07 Hash Tables
Data Structures
A DBMS uses various data structures for many different parts of the system internals.
Some examples include:
- Internal Meta-Data: Information about the database and the system state
- Core Data Storage: The actual data (tuples) we want to store
- Temporary Data Structures: Temporary data structures while processing a query to speed up execution (eg, hash tables for join)
- Table Indices: Auxiliary data structure to find specific tuples
There are two main design decisions to consider when implementing data structures for the DBMS:
- Data organization: How to layout memory and what information to store inside the data structure for efficient access.
- Concurrency: How to enable multiple threads to access the data structure without causing problems, ensuring that the data remains correct.
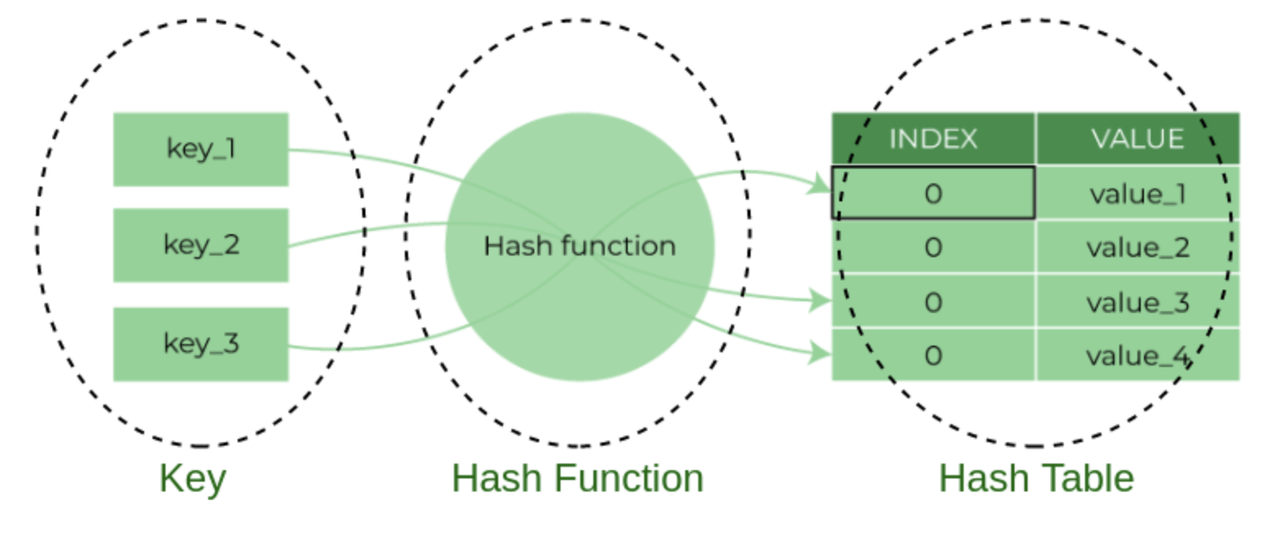
Hash Table
A hash table implementation is compromised of two parts:
Hash Functions tell us how to map a large key space into a smaller domain.
On one extreme, we have a hash function that always returns a constant (very fast, but everything is a collision). On the other extreme, we have a “perfect” hashing function where there are no collisions, but would take extremely long to compute. The ideal design is somewhere in the middle.
Hashing Schemes tell us how to handle key collisions after hashing.
Here, we need to consider the trade-off between allocating a large hash table to reduce collisions and having to execute additional instructions when a collision occurs.
Perfect hashing is generally more practical in situations where:
- The set of keys is completely known and does not change over time.
- The cost of computing the hash function during setup is justified by the benefits of the very fast query performance after setup.
Hash Functions
The DBMS need not use a cryptographically secure hash function (e.g., SHA-256) because we do not need to worry about protecting the contents of keys. These hash functions are primarily used internally by the DBMS and thus information is not leaked outside of the system. In general, we only care about the hash function’s speed and collision rate.
Static Hashing Schemes
A static hashing scheme is one where the size of the hash table is fixed. This means that if the DBMS runs out of storage space in the hash table, then it has to rebuild a larger hash table from scratch, which is very expensive. Typically the new hash table is twice the size of the original hash table.
To reduce the number of wasteful comparisons, it is important to avoid collisions of hashed key. Typically, we use twice the number of slots as the number of expected elements.
The following assumptions usually do not hold in reality:
- The number of elements is known ahead of time.
- Keys are unique.
- There exists a perfect hash function.
Therefore, we need to choose the hash function and hashing schema appropriately.
Linear Probe Hashing
This is the most basic hashing scheme. It is also typically the fastest.
Explanation:
When a collision occurs, we linearly seach the adjacent slots until an open one is found. For lookups, we can check the slot the key hashes to, and search linearly until we find the desired entry. If we reach an empty slot or we iterated over every slot in the hash table, then the key is not in the table. Note that this means we have to store both key and value in the slot so that we can check if an entry is the desired one. Deletions are more tricky. We have to be careful about just removing the entry from the slot, as this may prevent future lookups from finding entries that have been put below the now empty slot.
There are two solutions to this problem:
• The most common approach is to use “tombstones”. Instead of deleting the entry, replace it with a “tombstone” entry which tells future lookups to keep scanning.
• The other option is to shift the adjacent data after deleting an entry to fill the now empty slot. However, we must be careful to only move the entries which were originally shifted. This is rarely implemented in practice as it is extremely expensive when we have a large number of keys.
Non-unique Keys: In the case where the same key may be associated with multiple different values or tuples, there are two approaches.
• Separate Linked List: Instead of storing the values with the keys, we store a pointer to a separate storage area that contains a linked list of all the values, which may overflow to multiple pages.
• Redundant Keys: The more common approach is to simply store the same key multiple times in the table. Everything with linear probing still works even if we do this.
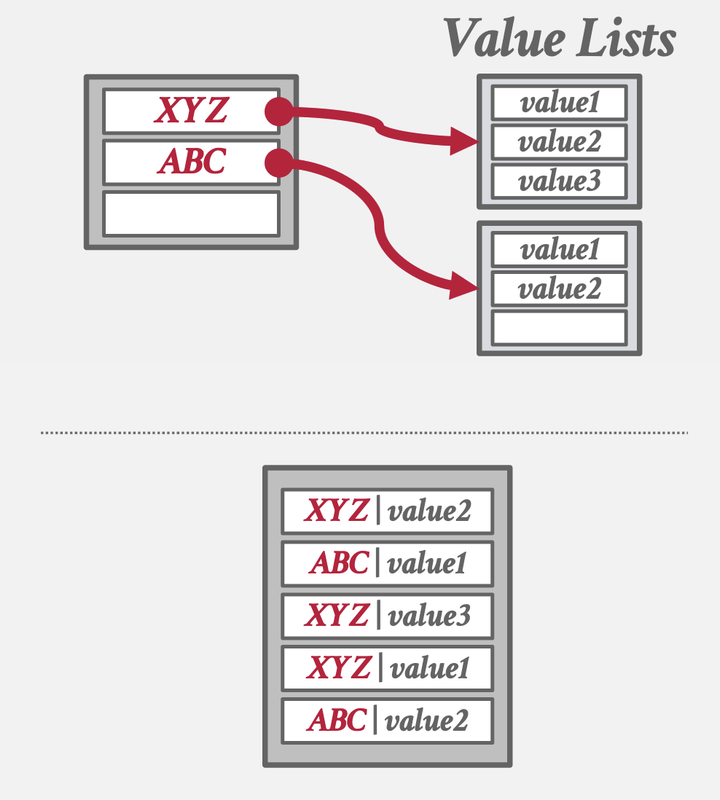
If you want to delete, you would also need to know the value in non-unique keys. Then, what is the point of this hash if you need to know the value in advance? This structure is good if you want to make joins.
Optimizations:
(I don’t understand this in depth)
- Specialized hash table implementations based on the data type or size of keys:
- Example: Maintain multiple hash tables for different string sizes for a set of keys and only a pointer or hash for larger strings.
- Storing metadata in a separate array:
- Example: Packed bitmap tracks whether a slot is empty/tombstone. This would help us avoid looking up deleted keys.
- Maintaining versions for the hash table and its slots:
Since allocating memory for a hash table is expensive, we may want to reuse the same memory repeatedly. To clear out the table and invalidate its entries, we can increment the version counter of the table instead of marking each slot as deleted/empty. A slot can be treated as empty if there is a mismatch between the slot version and table version.- Example: If table version does not match slot version,then treat the slot as empty.
Cuckoo Hashing
Use multiple hash functions to find multiple locations in the hash table to insert records.
- On insert, check multiple locations and pick the one that is empty.
- If no location is available, evict the element from one of them and then re-hash it find a new location.
Cuckoo hashing guarantees O(1) lookups and deletions, but insertions may be more expensive.
The essence of cuckoo hashing is that multiple hash functions map a key to different slots. In practice, cuckoo hashing is implemented with multiple hash functions that map a key to different slots in a single hash table. Further, as hashing may not always be O(1), cuckoo hashing lookups and deletions may cost more than O(1).
Note: There is another version of cuckoo hashing where there are two hash tables.
Dynamic Hashing Schemes
Dynamic hashing schemes are able to resize the hash table on demand without needing to rebuild the entire table. The schemes perform this resizing in different ways that can either maximize reads or writes.
Chained Hashing
The DBMS maintains a linked list of buckets for each slot in the hash table.
To look up an element, we hash to its bucket and then scan for it. This could be optimized by additionally storing bloom filters in the bucket pointer list, which would tell us if a key does not exist in the linked list and help us avoid the lookup in such cases.
Extensible Hashing
Improved variant of chained hashing that splits buckets instead of letting chains to grow forever.
UCI Professor Chen Li’s ASTERIX DB is one of the most well known databases that uses extensible hashing.
Linear Hashing
Instead of immediately splitting a bucket when it overflows, this scheme maintains a split pointer that keeps track of the next bucket to split. No matter whether this pointer is pointing to the bucket that overflowed, the DBMS always splits.
Taught in CS 122C by Professor Chen Li in UCI
Personal Notes
In general, we only care about the hash function’s speed and collision rate.
Linear Probe Hashing with Non-unique keys was a bit confusing (the concept of storing both key and value in the slot) not knowing how it would be used in the database system. I guess mostly for joining tables?
I was not aware until this lecture that Asterix DB was this popular among academics.